2024-05-28 14:24:32 临沧华图考试网 http://lincang.huatu.com/ 文章来源:云南华图

1. 【答案】C
【解析】第一步,本题考查最值问题,属于抽屉原理类。
第二步,本题要求任意分成4组,总会至少有一组的男生多于2人,构造最不利情况,即每一组都刚好差一点才能符合要求,也就是每一组都是2个男生,此时男生一共8人,在这个基础上加一名男生即可满足题干要求,所以参赛男生至少有8+1=9人。
因此,选择C选项。
【拓展】抽屉原理也叫最不利构造,核心思想是构造出差一点才能符合要求的情况,+1就是正确答案。
2.【答案】C
【解析】第一步,本题考查最值问题。
第二步,每个部门得到的奖品数量都不一样,又要使奖励的部门最多,每个部门越少越好,从1开始,1+2+3+4+5+6=21,若再发给一个部门,至少还需要7个奖品,21+7=28>25,不满足条件,所以最多6个部门。
因此,选择C选项。
3. 【答案】D
第一步,本题考查最值问题。
第二步,三个人一共下了7+6+5=18局,因为一局是两个人下,所以总共下了9局。因为老齐下了7局,所以老王和老周下了2局,同理可得,老齐和老周下了3局,老齐和老王下了4局。发现每个人和两个人下了,则途中至少要换两次人,所以至少有2局分出了胜负才能换人。
因此,选择D选项。
4. 【答案】C
【解析】第一步,本题考查最值问题,属于最不利构造类。
第二步,最不利构造答案=最不利情况+1,题中最不利的情况是取出了1个红色、1蓝色和1个绿色,因此答案=1+1+1+1=4(次)。
因此,选择C选项。
5. 【答案】B
【解析】第一步,本题考查最值问题。
第二步,由甲浇了30棵,乙浇了75棵,丙浇了80棵,丁浇了90棵,则100棵树共被浇水30+75+80+90=275(次),平均每棵树被浇275÷100=2.75(次),为了让被浇1次的树最多,那么被浇4次的树尽量多,因为甲只浇了30颗,所以被浇4次的最多为30棵,那么余下70棵树共被浇275-30×4=155(次),平均每棵树被浇155÷70≈2.21(次),说明需要一些树被浇3次才可以。
第三步,假设70棵树都被浇3次,那么多出70×3-155=55(次),每棵树少浇2次变为被浇1次,最多可以变为100-(1+42+30)=27(次)。
因此,选择B选项。
6.【答案】B
【解析】第一步,本题考查最值问题,属于最不利构造类。
第二步,从5名候选人中任意选两名共有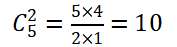 (种)选择方式。要保证有不少于5人推荐,即最不利情况+1,最不利的情况是每种方式都有4人,最终再加1,至少要有4×10+1=41(人)参加。
(种)选择方式。要保证有不少于5人推荐,即最不利情况+1,最不利的情况是每种方式都有4人,最终再加1,至少要有4×10+1=41(人)参加。
因此,选择B选项。
7. 【答案】B
【解析】第一步,本题考查最不利构造。
第二步,最不利构造问题的解=最不利+1。因此先构造出最不利的情况:拿了5次,5种颜色的球各拿了一个;此后,再拿出1个球,一定即可满足条件。
第三步,从其中拿5+1=6(次)能够保证至少有两个球的颜色一样。
因此,选择B选项。
8.【答案】B
【解析】第一步,本题考查最值问题,属于抽屉原理。
第二步,由开票发现前30张选票中,小超有15票,小刚有10票,小留有5票。要使小超一定当选,即不管剩下的两位各自获得多少票,小超都比他们票多,但目前小刚已得10票,威胁最大。最不利情形为:剩余30票中,除小超得到的票之外的其余票,全部被小刚所得。设小超在剩下30票中得票为x票,则小刚得票为(30-x)票,则可列不等式,解得x>12.5(票),要使小超在尽可能得票少的情况下当选,则取13票即可。
因此,选择B选项。
9.【答案】C
【解析】第一步,本题考查最不利构造问题。
第二步,由题干中出现“至少……保证”可知本题考查最不利构造问题,最不利值+1即为答案,由题目可知购买的数量分别为“7,2,9,11,8”,则最不利值=5+2+5+5+5=22;答案=22+1=23。
因此,选择C选项。
10.【答案】B
【解析】第一步,本题考查最值问题,属于最不利构造。
第二步,要保证有两个球的颜色相同,最不利的情况就是每种颜色的球各拿一个,抽奖箱有三种颜色的球,则共拿出了3个,此时再任意拿一个就能满足有2个球的颜色完全相同。至少拿出了3+1=4个,就能保证有两个球的颜色相同。
因此,选择B选项
(编辑:xufurong)